ちょっと休憩室
スリザーリンク
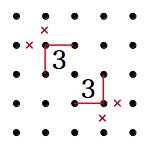
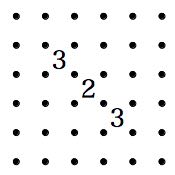
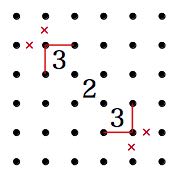
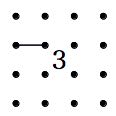
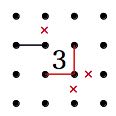
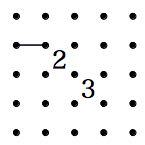
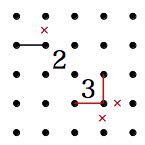
推測・考察
難問に行き詰まった時にどこを見たらよいか、また打開策を解説します。
１．「2」の斜め透過の法則。（私が勝手につけた名前です）
「2」は斜め方向に線が透過するように見える性質があります。
何を言っているのか分からないと思いますので、図で説明します。
-
-
斜め3と3
-
⇒
-
-
-
-
間に2が入っても
-
⇒
-
両側の結果は同じ
-
-
-
3に線1本
-
⇒
-
-
-
-
間に2が入っても
-
⇒
-
両側の結果は同じ
-
上の2つの例のように、間に「2」を入れても両側の結果は同じになります。
あたかも、線が「2」を斜めに透過しているようなイメージになります。
「2」を透過するという事は、「2」はいくつ入っていても両側の結果は同じになる事になります。
２．袋小路に線を入れない。
ループを作るということは、入った線は、出ていかなければなりません。
つまり、入れるところが一か所の場合、そこに入ってはいけないという事です。
その入口には、迷わず×を付けましょう。
３．そこに線を入れると、小ループにならないかを考える。
ループは1つだけというルールがあります。
そこに線を入れると、ループができるが、まだ他に線がある
又はまだ線を引かなければならない所がある場合
ループが2つ以上出来てしまうためそこには線は引けません。×を付けましょう。
すぐ出来なくても、線を引いていくといずれ小ループになる場合も同じです。
４．入る線は偶数
周りが閉ざされた空間ができた場合、そこに入り込む線の数は偶数でなければなりません。
線は、入ってきたら出ていかなければなりません。だから必ず偶数になります。
という事は、閉ざされた空間に一ヶ所入れる場所があった場合、
そこに入るか入らないかの判断に、今入っている線の数を数えることで対応できます。
つまり、奇数であれば入る（線を引く）偶数であれば入らない（×を付ける）事になります。
取り敢えずはこんな所でしょうか。
なんだか良く分からないという方もおられるでしょうが、問題を解いているうちに分かってくると思います。
たくさん問題を解いて、経験を積んでください。
ご自分で方法を発見する参考に、こんなことが書いてあったと覚えておいていただければと思います。
それでは、頑張って楽しんで問題を解いてください。
必要ないとは思いますが、練習問題の解答画像を置いておきます。
-
3x3-1
-
3x3-2
-
3x3-3
-
3x3-4
-
3x3-5
-
3x3-6
